가끔 알고리즘 문제를 풀다보면 2차원 배열을 90도 회전시켜야 하는 문제가 있습니다.
2차원 배열을 90도, 180도, 270도 회전시키는 방법을 알아봅니다.
N * N 배열에서의 90도 회전
가로, 세로가 같은 n * n 배열에서는 좀더 쉽게 회전시킬 수 있습니다.
심지어 별도의 배열을 선언하지 않고 해당 배열의 값을 직접 회전시킬 수 있습니다.
아래 그림처럼 기준 선을 잡고 맞은편의 숫자들을 한번씩 교환해주면 됩니다.

Java Code
public void rotate(int[][] matrix) {
int n = matrix.length;
// reverse up and down
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < n; j++) {
int temp = matrix[i][j];
matrix[i][j] = matrix[n - i - 1][j];
matrix[n - i - 1][j] = temp;
}
}
// reverse diagonally
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
}90도 회전
회전시키려는 arr 2차원 배열이 있습니다.
이 배열을 직사각형처럼 생각하면 90도 회전시켰을 때 가로, 세로가 바뀌게 됩니다.
따라서 가장 먼저 할 일은 배열의 n, m 을 바꾼 rotate 배열을 선언합니다.
그 후에 이중 for 문을 돌면서 rotate[i][j] = arr[n-1-j][i] 식으로
rotate 배열을 전부 채워주면 됩니다.
Java Code
// 90 rotate
static int[][] rotate(int[][] arr) {
int n = arr.length;
int m = arr[0].length;
int[][] rotate = new int[m][n];
for (int i = 0; i < rotate.length; i++) {
for (int j = 0; j < rotate[i].length; j++) {
rotate[i][j] = arr[n-1-j][i];
}
}
return rotate;
}90도, 180도, 270 도 회전
사실 90도 회전만 알아도 2번, 3번 반복으로 180도, 270도를 할 수 있지만
내친김에 나머지도 구현해보았습니다.
rotate 함수에서 degree 파라미터로 90, 180, 270 을 받아
회전시키는 함수입니다.
Java Code
static int[][] rotate(int[][] arr, int degree) {
int[][] rotate;
int n = arr.length;
int m = arr[0].length;
switch (degree) {
case 90:
case 270:
rotate = new int[m][n];
break;
case 180:
rotate = new int[n][m];
break;
default:
throw new IllegalArgumentException();
}
for (int i = 0; i < rotate.length; i++) {
for (int j = 0; j < rotate[i].length; j++) {
switch (degree) {
case 90:
rotate[i][j] = arr[n-1-j][i];
break;
case 180:
rotate[i][j] = arr[n-1-i][m-1-j];
break;
case 270:
rotate[i][j] = arr[j][m-1-i];
break;
}
}
}
return rotate;
}전체 소스코드
class Main {
public static void main(String[] args) {
int[][] arr = {
{1, 0, 0},
{1, 1, 1},
{1, 0, 1},
{1, 0, 1}
};
print(arr);
int[][] rotateArr;
System.out.println("\n90");
// 90 rotate
rotateArr = rotate(arr, 90);
print(rotateArr);
System.out.println("\n180");
// 180 rotate
rotateArr = rotate(arr, 180);
print(rotateArr);
System.out.println("\n270");
// 270 rotate
rotateArr = rotate(arr, 270);
print(rotateArr);
System.out.println("\n360 (90 rotate)");
// 90 rotate
rotateArr = rotate(rotateArr);
print(rotateArr);
}
static int[][] rotate(int[][] arr, int degree) {
int[][] rotate;
int n = arr.length;
int m = arr[0].length;
switch (degree) {
case 90:
case 270:
rotate = new int[m][n];
break;
case 180:
rotate = new int[n][m];
break;
default:
throw new IllegalArgumentException();
}
for (int i = 0; i < rotate.length; i++) {
for (int j = 0; j < rotate[i].length; j++) {
switch (degree) {
case 90:
rotate[i][j] = arr[n-1-j][i];
break;
case 180:
rotate[i][j] = arr[n-1-i][m-1-j];
break;
case 270:
rotate[i][j] = arr[j][m-1-i];
break;
}
}
}
return rotate;
}
// 90 rotate
static int[][] rotate(int[][] arr) {
int n = arr.length;
int m = arr[0].length;
int[][] rotate = new int[m][n];
for (int i = 0; i < rotate.length; i++) {
for (int j = 0; j < rotate[i].length; j++) {
rotate[i][j] = arr[n-1-j][i];
}
}
return rotate;
}
static void print(int[][] arr) {
for (int i=0; i<arr.length; i++) {
for (int j=0; j<arr[i].length; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
}
}출력
1 0 0
1 1 1
1 0 1
1 0 1
90
1 1 1 1
0 0 1 0
1 1 1 0
180
1 0 1
1 0 1
1 1 1
0 0 1
270
0 1 1 1
0 1 0 0
1 1 1 1
360 (90 rotate)
1 0 0
1 1 1
1 0 1
1 0 1'알고리즘 문제 > 공부' 카테고리의 다른 글
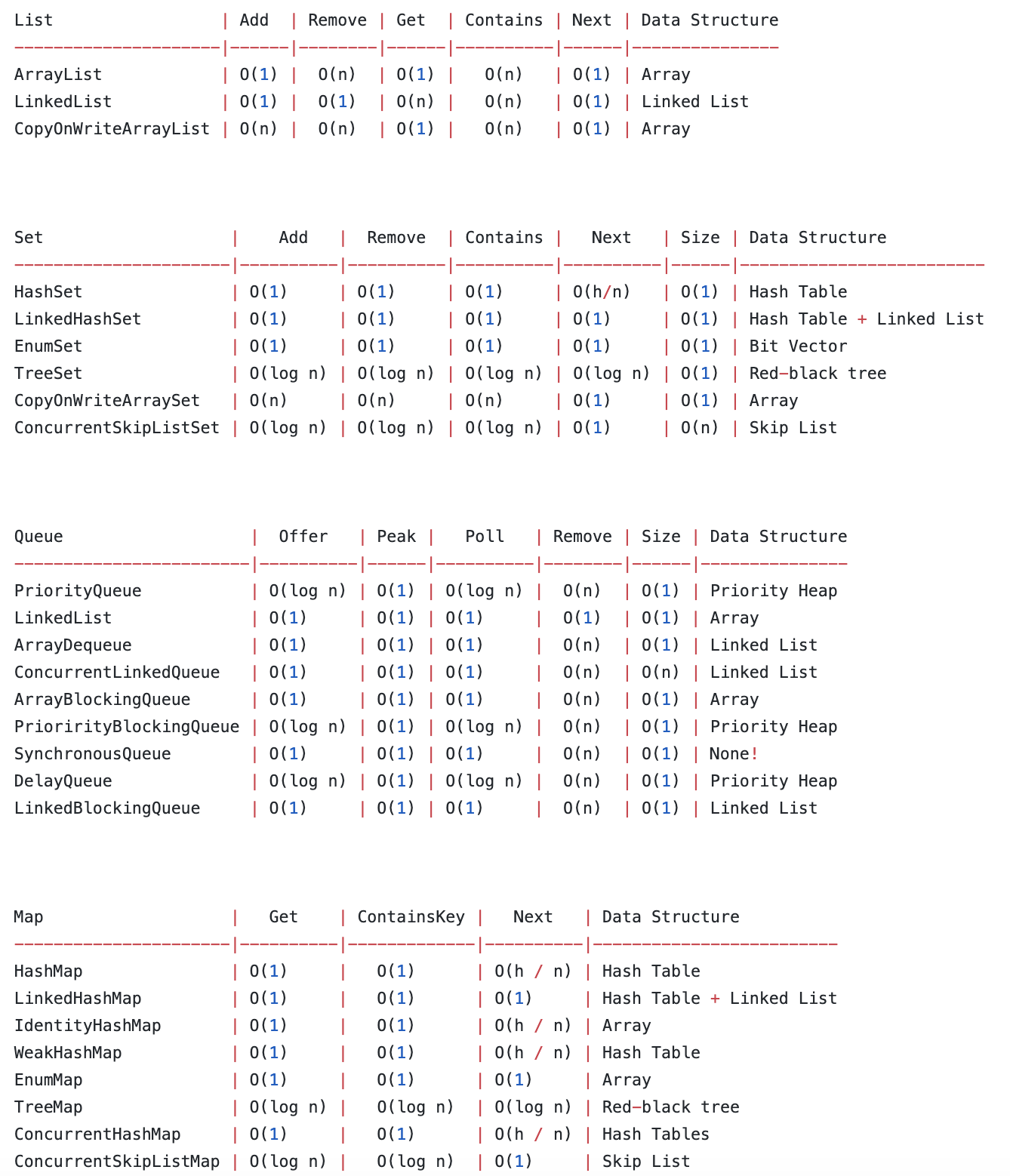
| 자바 Collections 시간복잡도 (Big-O) (0) | 2019.04.02 |
|---|---|
| 자바 출력 (Java) (0) | 2019.01.05 |
| 자바 입력 (Java) (0) | 2019.01.05 |
| 위상정렬 Topological Sort (Java) (1) | 2018.12.28 |
| 부분집합 PowerSet (Java) (2) | 2018.12.27 |